之前讲了开普勒轨道如何参数化，并且给出了一套可以解决经典参数化算法中的所有奇点的新参数化算法。这里不再赘述，具体可以看上一部分的序章和最后的间章内容。
啊……
但有了参数化算法问题只是解决了一半。必须还要能够反参数化，也就是从轨道参数计算出行星的位置和速度，这套算法才能实用。
另外再次重申（非常重要）：本文（以及上一篇文章）所有的形如 \(\arctan\frac{y}{x}\) 的反正切都定义为 \( \arg(x+\mathrm{i}y)\)，即为二元 \(\arctan\) 函数。如果没有搞清楚这个，先算了 \(y/x\) 再塞进 \(\arctan\)，一堆公式就会报废，出现各种不知所谓的错误。
第四章 开普勒轨道的反参数化
反参数化是参数化的逆过程。将参数化算法逆序，依次反解各个过程中出现的中间参数，即可完成反参数化。
根据第一部分的算法，开普勒轨道可用如下六个参数描述：
1. 倾角 \(i\)
2. 升交点经度 \(\Omega\)
3. 近点辐角 \(\omega\)
4. 角动量 \(j\)
5. 修正形状参数 \(q_0\)
6. 约化平近点角 \(m\)
首先，轨道形状参数 \(q\) 和偏心率 \(e\) 可直接从修正形状参数 \(q_0\) 计算得出：
\[q=q_0(q_0+2)\] \[e=q_0+1\]
对 \(q\lt 0\) 的情形，行星轨道为封闭的椭圆，约化平近点角 \(m\) 具有周期 \(T_m=2\pi/(-q)^{3/2}\)。必须在此时利用这一周期修正 \(m\) 使得 \(|m|\le T_m/2\)。这一修正的必要性之后会讲到。
接下来，应该根据约化平近点角 \(m\) 计算参数化中出现的过程量 \(x\) 和 \(y\)。由于 \(m\) 是 \(y\) 的奇函数，所以为了简化求解，以下仅考虑 \(m\ge 0\)。对 \(m\lt 0\) 必须取其绝对值再计算，得出结果后再将 \(y\) 反号，否则以下某些公式或者算法将会出错。
\(m\) 的完整表达式如下：
\[m=\left\{\begin{array}{ll}
y(\frac{y^2+3}{6}-\frac{3y^4+5}{40}q+\frac{5y^6+7}{112}q^2), &\mathrm{if}\;|(2-x)q|\lt 6\epsilon^{1/4} \\
\frac{ey}q-\frac{1}{q\sqrt{-q}}\arctan\frac{y\sqrt{-q}}{e-qx}, &\mathrm{else\;if}\;q\lt 0 \\
\frac{ey}q-\frac{1}{q^{3/2}}\mathrm{arcsinh}\left(y\sqrt{q}\right), &\mathrm{else}
\end{array}
\right.
\]
其中 \(\epsilon\) 为浮点相对误差，对 IEEE double，\(\epsilon\approx 10^{-16}\)；\(x\) 与 \(y\) 满足关系
\[x=\frac{\cos\theta}{1+e\cos\theta}\quad y=\frac{\sin\theta}{1+e\cos\theta}\]
\(\theta\) 为真近点角。
此时遇到的第一个问题是，\(m\) 的计算式中出现了三个分支，应该选取哪一分支继续求解。其中后两个分支分别对应椭圆轨道 \((q\lt 0)\) 和双曲线轨道 \((q\gt 0)\)，可以利用 \(q\) 的正负性轻易判断。而第一分支对应近似抛物线轨道 \((q\approx 0)\) ，其判断较为复杂。
考虑到对近似抛物线轨道，\(e\approx 1\)，\(q\approx 0\)，\(y^2\approx 1-2x\)。\(m\) 的计算式中第一个分支成为
\[m\approx\frac{y(y^2+3)}{6},\quad\mathrm{if}\;|(y^2+3)q|\lt 12\epsilon^{1/4}\]
该式仅与 \(y\) 有关。于是可以首先假定行星轨道为近似抛物线，根据该式从 \(m\) 求解出 \(y\)，再判断 \(y\) 是否满足该式成立的条件。如果满足，则行星轨道确实可近似为抛物线，应该使用 \(m\) 的完整表达式中的第一分支继续精确求解；否则便应根据 \(q\) 的符号，分别使用椭圆轨道 \((q\lt 0)\) 和双曲线轨道 \((q\gt 0)\) 的求解方法。
上式是一个关于 \(y\) 的三次方程，可以使用公式直接写出解：
\[y_0=\left(3m+\sqrt{1+9m^2}\right)^{\frac 1 3}-\frac 1{\left(3m+\sqrt{1+9m^2}\right)^{\frac 1 3}}\]
之前说到对 \(q\lt 0\) 的椭圆轨道，必须预先利用 \(m\) 的周期性尽可能降低 \(|m|\)，就是因为偏心率接近 \(1\) 的极端椭圆轨道在近点附近有时利用抛物线近似会更加精确。如果此时 \(m\) 中含有超大的周期，此处就会解出超大的 \(y_0\)，无法正确利用判据启用抛物线近似。
第4.1节 if \(|(y_0^2+3)q|\lt 12\epsilon^{1/4}\)：
此时进入抛物线轨道分支。以前述计算所得的 \(y_0\) 为初始值，使用牛顿迭代法，求解该分支 \(m\) 的表达式：
\[m=y(\frac{y^2+3}{6}-\frac{3y^4+5}{40}q+\frac{5y^6+7}{112}q^2)\]
即可获得 \(y\) 值。
由于近似抛物线轨道中，\(q\approx 0\)，\(y_0\) 已经是一个非常好的近似值，所以牛顿迭代的收敛将非常迅速，每次迭代的误差量应该迅速缩小（二次收敛）。在具体程序实现上，可以在每次迭代得到新的 \(y\) 后计算误差量 \(\Delta m=m(y)-m\)，如果某次迭代后 \(|\Delta m|\) 大于等于上一次，说明此时数值误差已经占据主导，牛顿迭代可以退出，并将最后一次迭代之前所得 \(y\) 值，即对应 \(\Delta m\) 最小的一个 \(y\) 值作为最终结果输出。
解得 \(y\) 后，可根据 \(x\) 与 \(y\) 满足的与真近点角 \(\theta\) 相关的关系解析计算得到 \(x\)：
\[x=\frac{1-y^2}{e+\sqrt{1+qy^2}}\]
第4.2节 else if \(q\lt 0\)：
此时进入椭圆轨道分支。可以计算经典的平近点角：
\[M=(-q)^{3/2}m\]
由之前对 \(m\) 的修正，此时应该有 \(0\le M\le\pi\)。
以 \(E_0=(6M)^{1/3}\) 为初始值，使用牛顿迭代法求解方程 \(M=E-e\sin E\) 得到偏近点角 \(E\)。这一初值的选取是合适的，迭代过程的余误差应该恒定减小，故迭代的终止条件可参考4.1节中描述。
解得偏近点角 \(E\) 后，\(x\) 与 \(y\) 可以如下解析计算：
\[x=\left\{\begin{array}{ll}\frac{1-y^2}{e+\cos E}, &\cos E\ge 0\\\frac{e-\cos E}{q}, &\cos E\lt 0\end{array}\right.\] \[y=\frac{\sin E}{\sqrt{-q}}\]
其中 \(x\) 的两个表达式是等价的，但分别会在极端椭圆轨道的远、近点，即 \(\cos E\approx\mp 1\) 且 \(e\rightarrow 1^-\) 时产生相近数值的抵消，导致严重误差。故应对 \(\cos E\) 的不同符号选用不同的形式计算。
第4.3节 else：
此时进入双曲线轨道分支。可以计算经典的平近点角：
\[M=q^{3/2}m\]
由之前对 \(m\) 的修正，此时应该有 \(M\ge 0\)。
令：\[E_0=\left\{\begin{array}{ll}
(6M)^{1/3}, &M\le \pi \\
\mathrm{arcsinh}(M/e), &M\gt \pi
\end{array}
\right.
\]
以 \(E_0\) 为初始值，使用牛顿迭代法求解方程 \(M=e\sinh E-E\) 得到偏近点角 \(E\)。这一初值的选取是合适的，迭代过程的余误差应该恒定减小，故迭代的终止条件可参考4.1节中描述。
解得偏近点角 \(E\) 后，\(x\) 与 \(y\) 可以如下解析计算：
\[x=\frac{1-y^2}{e+\cosh E}\] \[y=\frac{\sinh E}{\sqrt{q}}\]
End if.
——– 2023.7.17 更新 ——–
以上算法在牛顿迭代过程中，需要根据迭代自变量 \(y\) 或 \(E\) 求出 \(m\) 或 \(M\) 的值。由于在本文第一部分的更新内容中所述的原因，这些计算中可能存在一些精度损失，可以使用如下包含 \(\mathrm{kep}\) 函数的 \(m\) 的新表达式替代这些计算来避免：\[
c=\left\{\begin{array}{ll}
e-qx, &q\lt 0\\\sqrt{1+qy^2}, &q\ge 0\end{array}\right.\quad,\quad
m=\left\{\begin{array}{ll}
\frac{ey}q-\frac{1}{q\sqrt{-q}}\arctan\frac{y\sqrt{-q}}{c}, &c\lt 0\\
\frac{y}{1+e}+y^3\mathrm{kep}~c, &c\ge 0\end{array}\right.\quad.
\]
在椭圆或双曲线情形下，所求解的方程是关于偏近点角 \(E\) 与平近点角 \(M\) 而非 \(m\) 的，此时可按上式计算得到 \(m\) 后再计算 \(M=|q|^{3/2}m\) 。\(m\) 的表达式中存在的 \(y\) 与 \(c\) 也可由偏近点角 \(E\) 计算得到：对椭圆，有 \(y=\sin E/\sqrt{-q}\)， \(c=\cos E\)；对双曲线，有 \(y=\sinh E/\sqrt{q}\)， \(c=\cosh E\)。
注意 \(m\) 的计算式中 \(c\lt 0\) 的分支看起来较为复杂。由于在抛物线或双曲线中 \(c=\sqrt{1+qy^2}\gt 1\)，故仅有椭圆情形下可能用到 \(c\lt 0\) 的分支。此时该式直接使用偏近点角 \(E\) 表示时可以被进一步化简，最终结果即为直接计算 \(M=E-e\sin E\)，无需使用上式中 \(c\lt 0\) 时的复杂形式。
——– 更新完毕 ——–
此时，根据约化平近点角 \(m\) 求解参数 \(x\)、\(y\) 的过程已经完成，这也是反参数化算法中最为复杂的部分。需要注意如果求解前调整过 \(m\) 的符号，现在应该同样调整 \(y\) 的符号来恢复正确的结果。
现在可以直接写出在轨道参考坐标系中，行星的位置和速度矢量：
\[\vec r=\frac{j^2}{\mu}(x,y)\] \[\vec v=\frac{\mu}{j}\left(-\frac{y}{\rho},e+\frac{x}{\rho}\right)\]
其中 \(\rho=\sqrt{x^2+y^2}\)。
但此处需要注意，以上计算式中的 \(v_y\) 分量在行星位于高椭圆轨道的远点附近（自由落体轨道）时，会出现 \(e\approx 1\)，\(x\approx -\rho\) 的情况，该式成为 \(1-1\) ，直接计算会导致精度损失。在实际计算中，\(v_y\) 应该使用下式来代替计算以避免损失有效精度：
\[v_y=\frac{\mu}{j\rho}\left\{\begin{array}{ll}
e-qx, &q\le 0 \\
\sqrt{1+qy^2}, &q\gt 0
\end{array}
\right.
\]
目前计算所得的行星的位置矢量 \(\vec r\) 和速度矢量 \(\vec v\) 是在轨道参考坐标系中的结果。这一坐标系的 \(z\) 轴为轨道法向，\(x\) 轴为轨道的近点方向。使用前三个开普勒参数轨道倾角 \(i\)、升交点经度 \(\Omega\) 与近点辐角 \(\omega\) 可以在绝对坐标系中确定出轨道参考坐标系的朝向，进而可以将行星位置与速度转换至绝对坐标系，开普勒反参数化过程即正式完成。
第五章 轨道绘制算法
在计算机中，绘制轨道其实就是在轨道上选取有限多个点，然后用直线段将这些点依次连接起来。当选取的点足够多时，拼接的直线段就看起来与曲线轨道相差无几。在目前的绝大多数软件（如Space Engine, Kerbal Space Program等）中，选取点的算法是等平近点角间距选取（也即等时间间距选取），这样在偏心率接近 \(1\) 的椭圆或双曲轨道的近点附近，平近点角的微小变化可能导致真近点角数十上百度的变化，进而导致整个绘制结果呈现严重的折线化。而对严格的抛物线轨道，该方法完全失效。本章主要解决这个问题，并给出通用的、质量可控的轨道绘制算法。
定义法近点角 \(N\) 为轨道平面上，行星速度的垂线与轨道长轴的夹角：
\[N=\arctan\frac{-v_x}{v_y}\]
其中 \(v_x\) 与 \(v_y\) 可由上一章算法计算给出。
下图为几种近点角的定义的示意图。图中 \(O\) 为中心天体，\(A\) 为行星，红色椭圆为行星轨道，\(P\) 为近点。\(a\)、\(b\) 分别为轨道半长轴与半短轴， \(E\)、\(N\)、\(\theta\) 分别为偏近点角、法近点角与真近点角：
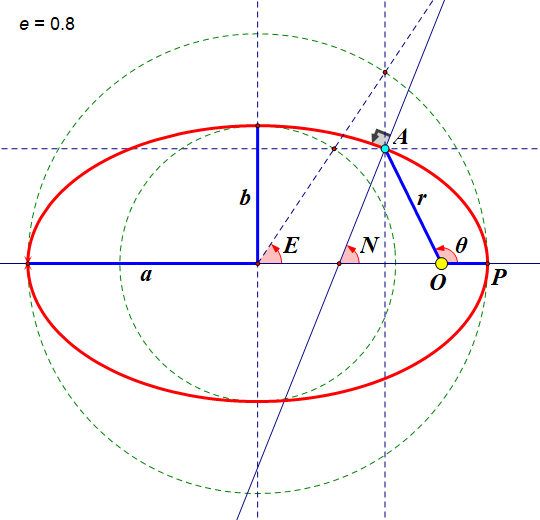
此时，只需要等间距选取法近点角，将各个法近点角对应的轨道位置用直线段连接起来，这些直线段之间的夹角就几乎是相同的定值，即事先选取的法近点角间距。这样就可以做到对任何轨道、任何位置都具有相同的绘制质量。
现在的问题还剩下两个：第一，如何确定法近点角的范围；第二：如何根据给定的法近点角，确定绘制点的位置。
这里不加证明地直接给出算法，具体过程留作习题懒得给了。
首先解决法近点角范围的问题。一般要绘制轨道时，绘制范围会受到中心天体希尔球半径 \(r_{h}\) 的限制。即使中心天体的影响范围无限，程序也应给出一个合理的绘制范围，以免极端椭圆轨道、抛物线轨道或双曲线轨道向无限远绘制，导致浮点溢出或其他错误。此时法近点角 \(N\) 的取值范围如下：
\[|N|\lt\arctan\frac{\sqrt{\max(qR^2+2R-1,0)}}{1+qR}\]
其中 \(R=\mu r_{h}/j^2\) 。
在上述法近点角的取值范围内等间距采样后，对任意法近点角值 \(N\)，对应的轨道位置可如下计算：
\[\beta=\sqrt{\cos^2 N-q\sin^2 N}\]
\[\frac{1}{\rho}=\beta\left\{\begin{array}{ll}
\beta+e\cos N, &\cos N\ge 0 \\
-\frac{q}{\beta-e\cos N}, &\cos N\lt 0
\end{array}
\right.\]
\[x=\frac{\beta\cos N-e\sin^2 N}{1/\rho}\]
\[y=\frac{\sin N}{\beta}\]
其中 \(\rho\)、\(x\)、\(y\) 满足关系
\[\rho=\frac{1}{1+e\cos\theta}\quad x=\frac{\cos\theta}{1+e\cos\theta}\quad y=\frac{\sin\theta}{1+e\cos\theta}\]
\(\theta\) 为真近点角。根据 \(x\) 和 \(y\) 可以直接写出绘制点在轨道参考坐标系中的坐标：
\[\vec r=\frac{j^2}{\mu}(x,y)\]
和上一章结尾一样，这个坐标可以用描述轨道朝向的三个参数转换到绝对坐标系中。所有绘制点的位置如上确定后，将它们依次用直线段连接起来，轨道绘制算法即宣告完成。
emmm
后面可能还有些总结性的东西或者数值例子，咕咕咕~~~
本文中描述的算法已全部使用c++实现，源代码发在 GitHub 上，相关类为ephem_orb，欢迎使用与测试~~
